"Archimedes' Limit:"

As I search to understand what makes calculus "tick," I have come to believe that its heart and soul are found in the limit concept. To me, this is what makes calculus both beautiful, and difficult.

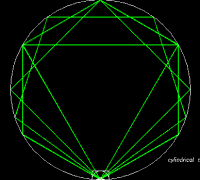
The most accessible illustration of this concept I can come up with is the example of regular polygons with n sides. The simplest member of this family is an equilateral triangle (n=3). Next comes a square, with n=4. As the process proceeds (n goes to infinity), almost everyone (including very young kids) can predict that the shape "at the limit" is a circle. Thinking of a circle as a regular polygon, with infinitely many, infinitely short sides has a very "calculus flavor." And while Archimedes was not using calculus when he used a very similar idea to try to calculate the exact value of Pi, his strategy of comparing the areas of inscribed and circumscribed polygons, certainly points toward the limit concept.

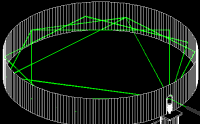
After presenting the Math Crew with this example, and challenging them to come up with a way of presenting it as an exhibit, a 15 year old member of the Crew presented his idea two days later: Put a laser inside of a cylindrical mirror. With the beam pointed at various angles, it will trace out a triangle, square, etc. When pointed just along the mirror surface, it will form a circle.

We tried out a few versions of this idea on a small scale, using a plastic gallon jug and some Mylar. It works!

The next step was to design a method that would allow the movement of a mirror for changing the beam angle:

Spurred on by the success of our initial trials, we turned to a more ambitious scale, using scavenged aluminum extrusion and Mylar:

The Mylar, while surprisingly effective, was extremely difficult to apply smoothly. After some research into affordable mirror solutions, we turned to "#8 mirror polish" stainless sheet. Installation of the stainless mirrors:

Initial trials with our new mirrors (using glycol fog):

Math Team members provided a lot of "sweat equity:"

...

...

...

...

...

Archimedes' Limit now resides in the "Calculus Pavilion," within the Museum's Experiment Gallery: